CoLA Kernels

[Project Paper] [Presentation] [Code]

CoLA, short for Compositional Linear Algebra, is a framework that tackles large-scale linear algebra tasks like matrix solves and eigenvalue problems in machine learning and scientific computing. While CoLA can automatically compose operations based on matrix structures (like sparsity or low-rank factorizations), its default Python-level implementations and dispatch mechanisms often lead to performance bottlenecks on GPUs. Below is a technical overview of how custom fused CUDA kernels can alleviate these bottlenecks and speed up select operations such as Arnoldi iterations, Cholesky decomposition, trace estimation, and SVD.

Motivation

High-Level Abstractions vs. GPU Intricacies

Many ML frameworks maintain abstraction layers (e.g., Python-level dispatch) that enable flexibility but introduce overhead. Launching numerous small GPU kernels results in underutilization of streaming multiprocessors (SMs) and frequent CPU-GPU synchronization. By writing specialized CUDA kernels that fuse multiple steps of an operation, significant speedups can be attained.

Memory Management Challenges

Iterative methods often create repeated memory allocations for intermediate results, causing fragmentations that slow overall performance. Fused kernels can reuse shared memory buffers. For example, Gram-Schmidt orthogonalization and matrix multiplications in Arnoldi iterations can be done with a single pass over data in well-structured kernels that reduce overhead.

Reduction in Synchronization

A single fused kernel launch means fewer synchronization points and fewer transitions between the CPU and GPU. These invisible costs often dominate runtime when matrix sizes grow large and the number of iterations increases.

Fused Kernel

Arnoldi Iteration

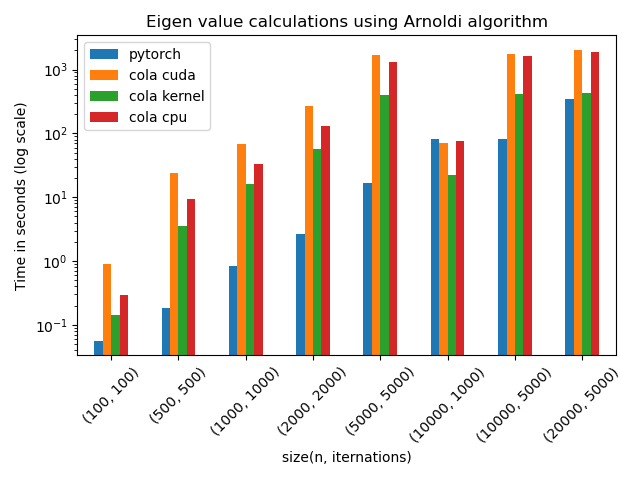
Arnoldi builds an orthonormal basis to approximate dominant eigenvalues. It requires matrix-vector multiplications and repeated Gram-Schmidt steps. A specialized fused kernel can privatize sums in shared memory, thereby avoiding multiple back-and-forth operations. Benchmarks showed up to 5x speedups compared to CoLA’s default GPU implementation, particularly when iterating over large matrices.

Cholesky Decomposition & Inverse

Cholesky factorization factors a positive definite matrix into L and Lᵀ, which can be inverted for solving linear systems more efficiently. A three-step CUDA approach: decompose_cholesky: Performs in-place diagonal updates and normalizes all relevant rows. inverse_lower: Inverts the lower triangular component. multiply_lower: Multiplies the invert to finalize the process. Although it required fewer kernel calls (only four total), careful use of cooperative groups and atomic operations meant the GPU version sometimes ran slower than PyTorch’s mixed CPU-GPU approach. However, it only required a fraction of the memory that PyTorch used.

Hutchinson Trace Estimation

Hutchinson’s method is a stochastic approach to approximate the trace of large matrices. An efficient variant uses random probes paired with fused matrix-vector multiplications and incremental summations. Current prototypes show that choosing optimal batch sizes, tolerances, and iteration counts is vital, as naive settings can cause high errors or underutilized GPU resources. Tuning these parameters promises more reliable convergence.

Singular Value Decomposition

By leveraging cuBLAS and cuSOLVER APIs, SVD computations can be accelerated significantly. In this project, the main GPU cost shifted from Python-level gather/scatter operations (e.g., transpose, clone) to the actual numerical routines. Profiling indicated that specialized kernels offloaded nearly all work to symmetrical matrix-vector operations (SYMV), reducing overhead and achieving 10x or more speedups for moderately sized matrices.

Observations and Key Takeaways

• Massive Kernel Launch Overhead Profiling indicated that frameworks sometimes launch dozens of kernels for a single operation, triggering repeated device synchronization and global memory thrashing. Consolidating these operations into fewer, larger kernels removed this overhead.

• Memory Allocation Efficiency Merged kernels absorb intermediate steps without writing temporary buffers to global memory. This reduces fragmentation and speeds up iterative operations that rely heavily on partial results.

• Trade-Offs in Implementation Complexity While specialized kernels outperform high-level libraries in many cases, they increase development overhead. For instance, PyTorch uses combined CPU-GPU routines to cleverly split tasks, which can sometimes outperform pure GPU approaches for certain matrix shapes or sizes.

• Tailoring Kernel Parameters Fusing is beneficial but not always straightforward. Choosing the right threads-per-block, balancing shared memory usage, and atomic operations all shape performance. Each kernel (e.g., Arnoldi vs. Cholesky) has different optimal configurations.

• Leveraging GPU Libraries Rather than reimplementing advanced methods from scratch, integrating libraries like cuBLAS and cuSOLVER for dense operations (gemm, eigendecompositions) often offers a fast path to speedups. The biggest gains then come from carefully orchestrating these calls with custom logic to minimize overhead.

Conclusion

Fusing multiple linear algebra operations into dedicated CUDA kernels can greatly reduce the kernel launch overhead and improve SM utilization. Although approaches like Arnoldi fusion achieve clear speedups, other methods (like Cholesky) highlight the nuanced interplay between heavy parallelism and algorithmic dependencies. For GPU-intensive tasks such as SVD, leveraging vendor libraries while reducing Python-level overhead has yielded significant performance benefits. There is still room for deeper optimizations—like more sophisticated kernel fusion heuristics and dynamic shape adaptations—but these initial results demonstrate that a carefully handcrafted CUDA approach can unlock considerable gains over compositional frameworks operating with off-the-shelf kernel calls.

This project underscores the principle that high-level abstractions, while convenient, must sometimes be supplemented or replaced by specialized GPU kernels to achieve peak performance in large-scale linear algebra.